Média, mediana ou menor valor? A justificativa da metodologia na pesquisa de preços em licitações e contratações públicas
Ricardo Silveira Ribeiro
Doutor em Direito Público pela UFPE
Subprocurador-Geral de Matéria Administrativa da ANP
Procurador Federal da AGU
Alterações recentes nas regras que regem a pesquisa de preços em contratações públicas não relacionadas com obras e serviços de engenharia trouxeram um grande desafio para o gestor público: justificar qual metodologia deverá ser utilizada para estimar os preços praticados no mercado.
Enquanto, na redação original da Instrução Normativa SLTI/MP nº 5, de 27 de junho de 2014, indicava-se que a pesquisa de preços deveria basear-se, em princípio, na média, as alterações decorrentes da Instrução Normativa SEGES/MP nº 3, de 20 de abril de 2017, deixam ao gestor a decisão de indicar a média, a mediana ou o menor dos valores como estimativa adequada do preço de mercado. Diante desse dilema, qual deve ser a escolha do gestor?
Antes de uma resposta, precisamos explicar ao leitor o que a média e a mediana significam. Ambas são medidas estatísticas que procuram resumir, com um só número, uma tendência em algo que está sendo analisado. Vamos pegar um exemplo do cotidiano da gestão pública para entendermos melhor.
Imagine que estamos tentando pesquisar preços de um uniforme básico de vigilância patrimonial para uma licitação. Após consultarmos os parâmetros indicados no art. 2º da Instrução Normativa SLTI/MP nº 5/2014, encontramos 7 (sete) preços distintos praticados por diferentes empresas: R$ 130,00, R$ 170,00, R$ 164,00, R$ 50,00, R$ 500,00, R$ 200,00 e R$ 162,00. Vamos então ordenar esses preços do menor para o maior para que você consiga visualizar o que está acontecendo: R$ 50,00, R$ 130,00, R$ 162,00, R$ 164,00, R$ 170,00, R$ 200,00 e R$ 500,00.
De acordo com o art. 2º, §§2º e 4º, da Instrução Normativa SLTI/MP nº 5/2014, o gestor deve examinar os preços coletados de forma crítica, isto é, não pode aceitar, cegamente, que esses preços representam os valores praticados pelo mercado. Deve verificar se não existem preços muito discrepantes do padrão.
Preços discrepantes do padrão são preços muito altos (excessivamente elevados) ou muito baixos (inexequíveis). No nosso exemplo, os uniformes que custam R$ 500,00 e R$ 50,00 estão claramente distantes do padrão, pois os preços tendem a oscilar entre valores intermediários significativamente diferentes desses extremos (ex.: R$ 162,00, R$ 170,00). Uma vez localizados esses preços extremos, deve-se então suprimi-los, pois não refletem aquilo que, efetivamente, está acontecendo no mercado. Esse é o comando do art. 2º, §§ 2º e 5º, da Instrução Normativa SLTI/MP nº 5/2014.
Feito isso, devemos passar à etapa seguinte – escolher a metodologia correta.
Primeiramente, na quase totalidade das situações, não se deve estimar os preços de mercado a partir do menor valor. Há uma razão técnica para isso: estatisticamente, o menor valor não representa a tendência dos preços de mercado. Representa, apenas, o valor mais barato dentre os preços coletados pelo gestor. Por não ser uma medida da tendência dos preços de mercado, não há suporte técnico para adotá-lo como regra geral, embora, em situações especiais, possa ser utilizado, como veremos mais abaixo.
Portanto, a primeira recomendação é esquecer o menor preço como parâmetro para a estimativa dos preços de mercado. As medidas estatísticas que, realmente, devem ser adotadas são a média e a mediana, pois se destinam a medir a tendência dos preços coletados na amostra; são o que, em Estatística, denominamos de medidas de tendência central. Segue precedente ilustrativo do TCU sobre o tema:
VOTO
22. Tanto a Secretaria de Obras quanto a de Recursos manifestaram-se pela manutenção das determinações, pugnando pela utilização da menor cotação dos preços na orçamentação da obra, em detrimento da mediana utilizada pelo TRT.
23. Em que pese a abalizada argumentação apresentada pelas unidades instrutivas, constantes do relatório precedente, divirjo do encaminhamento proposto.
24. Cumpre registrar que a Lei n.° 8.666/93 não prescreve como deve ser realizado este orçamento. A Lei de Diretrizes Orçamentárias, por sua vez, não prevê a forma pela qual será realizada a cotação de preços quando ausente o insumo no SINAPI e inexistente a tabela de referência formalmente aprovada por órgão ou entidade da administração pública federal.
25. Verifica-se, portanto, a existência de uma lacuna no ordenamento na medida em que os normativos não definem como será realizada a orçamentação de insumo quando este não estiver cotado no SINAPI e tampouco haja tabela de referência oficial.
26. Não me parece razoável a exigência de que a orçamentação nestes casos deva sempre considerar o menor preço cotado no mercado. Entendo que a utilização de preços médios ou da mediana, além de bem refletir os preços praticados no mercado, não implica ofensa à Lei de Licitações, à LDO/2009 ou aos princípios gerais da Administração Pública.
27. A colmatação da lacuna normativa efetuada pelos gestores do TRT utilizou-se do parâmetro legal esculpido no caput do art. 109 da LDO/2009 e, assim, definiu como custo unitário dos insumos a mediana dos preços pesquisados. A solução me parece dotada de razoabilidade, assim como seria se houvesse utilizado a média das cotações. Destaco que o menor preço é um dos preços do mercado, mas não reflete o mercado. Nesse sentido, entendo que o preço de mercado é mais bem representado pela média ou mediana uma vez que constituem medidas de tendência central e, dessa forma, representam de uma forma mais robusta os preços praticados no mercado (Acórdão nº 3.068/2010 - Plenário) (grifos nossos).
A principal dúvida é saber quando então escolher uma dessas medidas. Ora, a média dos preços representa a soma dos mesmos dividida pela quantidade de preços coletados:
![]()
No nosso exemplo, a soma dos preços coletados é R$ 826 (R$ 130,00 + R$ 162,00 + R$ 164,00 + R$ 170,00 + R$ 200,00). Por outro lado, foram coletados 5 preços de empresas diferente. Aplicando a fórmula, temos uma média de R$ 165,2. Isso significa que se a coleta de preços foi adequadamente realizada, o preço de mercado tenderá a ser R$ 165,2.
A mediana dos preços pesquisados, por outro lado, é o preço que está no meio dos preços coletados, quando os [1]ordenamos do menor para o maior (ou do maior para o menor). No nosso exemplo, o preço que está no meio é R$ 164,00, destacado em vermelho:
R$ 130,00 R$ 162,00 R$ 164,00 R$ 170,00 R$ 200,00
Percebam: como está no meio, o preço mediano divide os preços em duas partes iguais. No nosso exemplo, há dois preços do lado esquerdo e dois preços do lado direito. Se estivéssemos em uma grande avenida, o ponto mediano seria aquele que dividiria a avenida em duas partes iguais, ou seja, seria o ponto que estaria exatamente no meio.
A mediana fica fácil de detectar quando dispomos de um número ímpar de preços coletados, como o do exemplo acima. Se temos 3, 5, 7 ou 9 preços, é simples identificar a mediana quando ordenamos esses preços do menor para o maior valor. Contudo, se a quantidade de preços for par, não haverá um só número no meio. Por exemplo, imaginemos agora que tenhamos conseguido apenas preços de uniforme de quatro empresas:
R$ 130,00 R$ 162,00 R$ 170,00 R$ 200,00
Nesse caso, não haverá um só preço no meio que separe os demais preços em partes iguais, pois só conseguimos um número total de preços par – 4 (quatro) preços de empresas diferentes. O meio, portanto, está entre os preços R$ 162,00 e R$ 170,00. Se fôssemos usar uma reta para dividir o conjunto de preços exatamente no meio, a mediana ficaria localizada onde está esta reta:
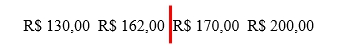
Acontece que nossa mediana aqui não é uma reta. É um número. Precisamos, em verdade, de um número que represente esse meio. Esse número, entretanto, não existe. Como fazer para contornar esse problema?
Os estatísticos desenvolveram uma solução: basta obter a média dos dois números que estão mais próximos do centro. No nosso caso, seria a média dos números que estão imediatamente dos lados esquerdo e direito de nossa reta. São os preços R$ 162,00 e R$ 170,00, grifados em vermelho:

A média dos dois preços mais centrais, R$ 162,00 e R$ 170,00, dá R$ 166,00. Esta é a nossa mediana: R$ 166,00.
Bem, agora podemos voltar a nosso exemplo original com cinco preços. Qual é a medida preferível, a média ou a mediana? Em geral, os livros de estatística dizem que não há uma medida preferível. Para nossos propósitos, contudo, a média tende a refletir melhor o conjunto dos dados, pois seu valor computa todos os preços coletados. Não despreza qualquer informação coletada e isso é uma grande vantagem estatística.[2] A regra geral, portanto, é usar a média como medida de tendência central. Essa, inclusive, é a medida usualmente adotada no dia a dia.
Contudo, há casos nos quais a mediana é a medida preferível. Particularmente, se você gestor ainda suspeita que existem valores significativamente diferentes do padrão, muito altos ou muito baixos, que não puderam ser excluídos da amostra por não serem claramente discrepantes, será melhor usar a mediana como medida de tendência central. A razão para isso é que a média é fortemente influenciada por valores extremos. Preços significativamente altos ou significativamente baixos podem afetar a média substancialmente, comprometendo os resultados da pesquisa de preços. A mediana, por outro lado, tende a ser pouco afetada por valores muito diferentes do padrão. Desse modo, na dúvida se ainda existe algum preço muito alto ou muito baixo, deve-se usar a mediana.
No nosso exemplo com cinco preços, a média deu R$ 165,2, enquanto a mediana foi de R$ 164,00. Como são preços não muito distantes, provavelmente não existem valores extremos e é recomendável adotar a média. Portanto, aqui vai outra lição: se a média e a mediana possuem valores muito próximos, não há com o que se preocupar. Isso é um bom sinal!
Suponhamos agora que encontramos os preços abaixo, que se diferenciam dos anteriores em razão de havermos substituído o preço de R$ 200,00 por R$ 300,00 na nossa cotação:
R$ 130,00 R$ 162,00 R$ 164,00 R$ 170,00 R$ 300,00
Pergunta-se: devemos utilizar a média ou a mediana?
Ora, R$ 300,00 parece ser um preço muito alto, mas temos dúvida se pode ser suprimido da amostra pelo procedimento previsto no art. 2º, §§2º e 5º, da Instrução Normativa SLTI/MP nº 5/2014. Na dúvida, a recomendação é adotar a mediana como medida de tendência central, pois ela é considerada uma medida resistente,[3] isto é, não é tão influenciada pela presença de um preço extremo.[4] Nesse sentido, note que a substituição do preço anterior de R$ 200,00 por R$ 300,00 não alterou a mediana, que continua a ser R$ 164,00. Essa substituição, contudo, afetou a média.
Na prática, o gestor pode fazer um rápido “teste” não formal para saber qual medida usar: pode calcular as duas medidas e informá-las no processo. Se elas forem relativamente próximas, isso significa que não há razão para se preocupar e a média poderá ser adotada.[5] Contudo, se essas duas medidas forem muito divergentes, haverá a evidência de que podemos estar diante de um preço extremo que está influenciando significativamente a média para mais ou para menos. Por essa razão, a média termina por ficar muito distante da mediana. Nessa circunstância, é melhor adotar a mediana, pois esta medida não se deixa influenciar por um preço extremo.
Voltando a nosso exemplo, a média dos cinco preços acima deu R$ 185,2, enquanto a mediana foi de R$ 164,00. Nesse caso, há uma diferença de apenas R$ 21,2 entre essas medidas. Não parece haver razão para adotarmos a mediana. Ficamos então com a média como referência.
Outra providência prática que poderá ser utilizada é a supressão do preço que o gestor julga ser muito alto ou muito baixo somente com o objetivo de simular como a média reagirá à ausência do preço. Se, após novo cálculo, o valor da média diminuir ou aumentar muito, use a mediana como medida de tendência central para sumarizar a tendência de todos os preços coletados.[6] Se a média mudou muito em razão da supressão do preço suspeito, isso significa que pode haver preço atípico influenciando seu cálculo.
Dito isso, cabe agora perguntar: e o menor valor? Quando usá-lo?
Como dissemos, não há fundamento técnico para usarmos o menor valor como medida da tendência dos preços no mercado. Desse modo, em regra, não deve ser usado. Há circunstâncias especiais, entretanto, nas quais pode ser usado como uma cautela da Administração Pública para não pagar preços excessivos. Isso se dá quando estamos diante de um bem ou serviço prestado por algumas poucas empresas em ambiente de baixa competição econômica. Seguem considerações do TCU nesse sentido:
VOTO
22. Concordo apenas em parte com o argumento da unidade técnica. Há inúmeras deliberações desta Corte em que se exigiu a realização de pesquisa de preços de mercado para balizar contratações públicas (acórdãos 89/2009, 1.198/2009, 265/2010, 2.967/2012 e 1.785/2013, todos do Plenário, entre tantos outros). Em sua imensa maioria, não se indicou ao gestor qual dos valores pesquisados adotar.
23. Por outro lado, há precedente deste Tribunal no sentido de que, pelo menos em alguns casos, deve-se adotar o preço médio ou mediano pesquisado, como se depreende do excerto abaixo, do voto condutor do acórdão 3.068/2010 – Plenário: [...]
24. O advérbio “sempre”, presente no trecho “não me parece razoável a exigência de que a orçamentação nestes casos deva sempre considerar o menor preço cotado no mercado” indica que, em muitos casos, devem-se adotar preços abaixo da média. Cabe ao gestor avaliar o caso e fazer sua opção, justificando-a.
25. No caso de produtos simples, comumente encontrados em lojas varejistas, o valor mínimo de uma cotação pode representar uma situação momentânea, de uma “liquidação”, por exemplo, e não corresponderá ao preço praticado quando da efetiva aquisição.
26. Por outro lado, quando são cotados equipamentos fornecidos exclusivamente por poucas empresas, de certo porte, deve-se sim adotar o mínimo valor cotado, pois é de se presumir que haja estabilidade nesses preços. É o caso de elevadores. Certamente, o preço cotado junto a uma Atlas, Otis ou outra congênere não representa uma “liquidação” ou promoção temporária.
27. Creio ser esse o caso dos barômetros aqui tratados, fornecidos por empresas multinacionais. Portanto, concordo com a unidade técnica de que deveria ter sido adotado o preço mínimo pesquisado como referência na licitação. Porém, não se mostra razoável pretender punir o gestor por ter adotado valor médio, quando não há – conforme reconhecido pela unidade técnica – nem mesmo jurisprudência sedimentada do TCU nesse sentido.
ACÓRDÃO
ACORDAM os ministros do Tribunal de Contas da União, reunidos em sessão da 2ª Câmara, ante as razões expostas pela relatora e com base no art. 237, inciso VII, do Regimento Interno, c/c o art. 113, § 1º, da Lei 8.666/1993 em:
[...]
9.2. notificar a Infraero de que, quando da pesquisa de preços de mercado para definição de valores referenciais de licitações, devem ser adotadas as cotações mínimas encontradas sempre que se tratar de insumo ou equipamento fornecido exclusivamente por um conjunto restrito de empresas; (Acórdão nº 7.290/2013 - 2ª Câmara) (grifos nossos).
O precedente acima foi ratificado em manifestações posteriores:
VOTO
Ao contrário do que alega a recorrente, o Acórdão 7290/2013 – TCU – 2ª Câmara considerou que, “quando são cotados equipamentos fornecidos exclusivamente por poucas empresas, de certo porte, deve-se sim adotar o mínimo valor cotado”, ainda que a decisão tenha reconhecido a inexistência de texto normativo ou jurisprudência nesse sentido.
Ressalto que a determinação questionada no recurso foi realizada somente com relação à desestatização do Bipolo-2 da Usina Hidroelétrica de Belo Monte/PA, tratada como situação “sui generis” no voto condutor do acórdão recorrido.
[...]
Como os argumentos recursais não foram suficientes para justificar a utilização da média das cotações para estimativa de investimento para os módulos de equipamentos principais das estações conversoras, fornecidos exclusivamente por poucas empresas, acolho integralmente a instrução da unidade técnica, nego provimento ao pedido de reexame e voto no sentido de que seja aprovado o Acórdão que ora submeto à deliberação deste Colegiado (Acórdão nº 644/2016 - Plenário).
VOTO
29. Com relação aos precedentes contrários ao uso dos custos incorridos pelo contratado como base para a obtenção do preço de referência, não se nega que esse é o entendimento correto à luz do regime jurídico dos contratos administrativos e do próprio sistema econômico do país que prega a liberdade de iniciativa e a busca do lucro.
30. Porém, em situações extremas como a que ora se enfrenta, em que não existem preços nos sistemas referenciais e o insumo analisado foi adquirido em um mercado monopolístico, julgo que o valor obtido das notas fiscais, acrescido de custos indiretos e BDI acima do atualmente aceito pelo TCU, constitui um parâmetro seguro do valor de mercado do bem. Tomando por base a ideia de abuso de direito e os princípios da boa-fé contratual e do não enriquecimento sem causa, entendo que os preços praticados pela contratada excedem o limite do razoável, não podendo ser considerados compatíveis com os de mercado (Acórdão nº 1.992/2015 - Plenário).
VOTO
90. Na linha do Acórdão 7290/2013-2ª Câmara (rel. Ministra Ana Arraes), entendo que, em se tratando de aquisição de equipamentos a serem fornecidos em mercado restrito, oligopolizado, deve ser adotada a cotação mínima e não a mediana. Isso porque, nesse tipo de mercado, dificilmente os menores valores decorrem de situações excepcionais, como promoções (Acórdão nº 1.639/2016 - Plenário) (grifos nossos).
Como se vê, há uma lição decorrente desses precedentes: a média e a mediana são as medidas a serem adotadas como regra. Excepcionalmente, o menor valor deve ser adotado como uma cautela para que se evite o pagamento de preços excessivos. Isso, particularmente, dá-se quando estamos em um ambiente de competição oligopolista.
Quando então reconhecer essa circunstância?
Se o setor da economia é dominado por poucas empresas que produzem determinado bem ou prestam serviço específico e há a necessidade de altos investimentos para entrada de novos concorrentes ou ainda dificuldades adicionais para o surgimento de novos competidores – barreiras de entrada –, há uma grande probabilidade de estarmos diante de uma situação de competição oligopolista.
Nesse ambiente econômico de competição entre poucos agentes, os preços de determinado bem ou serviço são fixados pela empresa estrategicamente, isto é, levando-se em consideração o modo como o outro concorrente irá reagir a esse preço. Há, portanto, interdependência entre os agentes econômicos.
Por essa razão, o comportamento estratégico de poucas empresas tem o poder de estabelecer o preço a ser praticado no mercado. Nesse sentido, o preço tende a ser, tecnicamente, rígido, pois não muda significativamente, mesmo com a alteração dos custos e da demanda por bens e serviços.[7] Por outro lado, como um competidor sabe que se baixar muito seu preço haverá uma tendência a outro competidor baixá-lo também, e assim sucessivamente, com redução substancial dos lucros de todos, a competição oligopolista termina acarretando incentivos para que as empresas fixem um preço considerado “razoável” para assegurar bons retornos econômicos.[8]
É nessa circunstância que o TCU recomenda a adoção do menor preço. Consequentemente, não se está tentando aqui estimar propriamente os preços de mercado, mas adotar um preço que possa servir de “defesa” contra a tendência de esse mercado estipular preços excessivos em razão da baixa presença de competidores.
Em suma, a média deve ser utilizada como regra geral, pois consegue levar em conta todos os preços coletados.[9] Se mesmo após suprimirmos os preços excessivos ou inexequíveis, ainda suspeitamos da existência de preços extremos, para mais ou para menos, devemos usar a mediana. Por fim, em mercados sujeitos à competição oligopolista, devemos usar o menor dos preços coletados na pesquisa.