UTILIZAÇÃO DA ESCALA DE FIBONACCI NA AVALIAÇÃO DE RISCOS: VANTAGENS, APLICAÇÕES E DIDÁTICA
Benedito Antonio da Costa
Analista Judiciário do TRE-MT. Mestrando em Direito pela UNOESC. Especialista em Direito Constitucional Eleitoral pela UnB. Especialista em Direito Ambiental pela Unemat. Especialista em Direito Administrativo pela Uniderp.
(o presente artigo também foi publicado no TRE-MT)
RESUMO
Este artigo revela os benefícios da utilização da Escala de Fibonacci para estimação da probabilidade e do impacto na etapa de avaliação de riscos, demonstrando a coerência e harmonia gerada na matriz de riscos. Propõe a utilização de auxílios visuais no momento da estimativa da probabilidade e do impacto. Por fim, sugere-se que o cálculo do risco residual seja feito com base na análise direta do controle existente sobre a probabilidade e o impacto. Em seu conjunto, o artigo pode ser considerado como uma metodologia de avaliação de riscos.
PALAVRAS-CHAVE: 1. Avaliação de riscos 2. Metodologia
3. Escala de Fibonacci 4. Didática
1. INTRODUÇÃO
Riscos estão presentes como fatores que impactam toda atividade humana. Avaliá-los corretamente pode ser a chave para o sucesso ou fracasso de uma atividade, processo, empreendimento ou mesmo de inteiras organizações.
Nem sempre é fácil fazer avaliação de riscos pelo método da multiplicação de escalas de probabilidade e impacto. Quantidades são difíceis de comparar. Tome-se como exemplo nossa quase inca- pacidade em fazer projeções de peso e volume em líquidos, a partir de certa quantidade apenas vista a olho nu. Avaliar, ou seja, julgar eventos quanto à probabilidade de ocorrência e quanto ao impacto que causará em um determinado sistema apresenta, por certo, um grande grau de dificuldade, principalmente quando o tratamento es- tatístico de dados não é possível ou não está disponível.
Para nosso alento, a ciência vem em nosso auxílio. As propor- ções da natureza e dos números nos auxiliam em todos os empreen- dimentos, como arquitetura, arte, tecnologia. Certamente, conforme demonstraremos aqui, nos ajudará na difícil tarefa de avaliar riscos e priorizar ações.
Primeiramente abordaremos a relevância do processo de ges- tão de riscos para as organizações, notadamente as públicas. Logo após ressaltaremos como a utilização de uma escala de valores apro- priada pode ter grande impacto no processo de avaliação de riscos.
2. A IMPORTÂNCIA DA GESTÃO DE RISCOS NOS PROCESSOS DE GOVERNANÇA E DE GESTÃO DE ORGANIZAÇÕES PÚBLICAS
A ideia de “função” e “agência” é especialmente forte quando se trata de organizações públicas, pois o detentor dos recursos está plasmado em todos os cidadãos e habitantes de determinado território[1]. A demanda por accountability é forte, e esta é muitas vezes presente, mas muitas vezes também mal demonstrada.
A prática da gestão de riscos corporativos, na Administração Pública, faz parte da demonstração do tipo de gestão que faz o agente público. Demonstra de uma só vez a razão de determinadas ações de gestão, a proporcionalidade das ações tomadas, as correções das respostas aos riscos identificados.
A gestão de riscos, além de demonstrar a existência da relação de accountability e demonstrar a gestão e governança dos recursos, tem efeitos muito diversos e positivos, como aqueles apontados pelo Committee of Sponsoring Organizations of the Treadway Comis- sion - COSO (2013):
1) efeitos no planejamento estratégico (alinha o ape- tite a risco com a estratégia;
2) torna claro e fortalece as decisões em resposta aos riscos;
3) reduz surpresas e prejuízos operacionais;
4) auxilia a identificar problemas sistêmicos ao identificar e administrar riscos múltiplos e entre empreendimentos;
5) auxilia no aproveitamento das oportunidades e;
6) otimiza o capital.
Assim, tendo em vista uma relação tão clara entre accountability e o processo de gestão de riscos, pode-se afirmar que a existência, manutenção e aperfeiçoamento de uma gestão de riscos seja condição sine qua non para uma gestão responsável da coisa pública e cumprimento de princípios constitucionais diversos, como a legalidade, impessoalidade, publicidade e eficiência.
Legalidade porque cada vez mais os normativos exigem que aja a implementação e funcionamento de processo e política de gestão de riscos nas organizações públicas, em todos os poderes da República. O Tribunal Regional de Mato Grosso, por exemplo, possui um normativo interno (Resolução TRE-MT nº 1719/2016) que determina a instituição de tal processo. Impessoalidade porque impede o agente de fazer gestão buscando finalidade outra que não atingir um objetivo ou mitigar um risco. Publicidade porque por meio das diversas avaliações, gradações, priorizações, comparações e análises, a sociedade toma conhecimento dos reais motivos das ações de gestão e das análises de seu cabimento em determinado contexto. Eficiência por motivos óbvios, pois expor determinado valor, recurso ou pessoas a riscos não controlados vai contra qualquer ideia de eficiência.
As práticas de accountability devem, portanto, ser ressaltadas e demonstradas para que se considere que o gestor age com respon- sabilidade, e entre as práticas que demonstram e geram accountability, uma das principais é a habilitação do processo de gerenciamento de riscos, compreendido por fases como a identificação, avaliação e resposta aos riscos.
O momento de identificação dos riscos é de relevada importância. É nela em que o gestor identifica a possibilidade (probabilidade) de ocorrência de eventos e estima os impactos que estes podem causar. Uma técnica apurada nesta fase pode fazer muita diferença em todo o processo de gerenciamento de riscos e, consequentemente, no alcance e proteção dos objetivos organizacionais (LEICH, 2008).
3. O RISCO: CONCEITOS BÁSICOS
A noção de risco é intuitiva: em seu sentido mais usual, geral- mente refere-se à probabilidade de insucesso de uma determinada ação ou alcance de um objetivo, porque algo de errado pode acontecer devido a fatores internos ou externos às atividades envolvidas[2]. A eventualidade de sua ocorrência e o impacto no objetivo são características marcantes. Tanto que, com uma concisão impressionante, NBR-ISO 31000 define risco como: “efeito da incerteza nos objetivos”.
Deve-se ter em mente, também, que toda a atividade, seja ela qual for e em relação a qualquer objetivo que seja, possui alguma probabilidade de ocorrência de algum evento que a impacte negativamente, motivo pelo qual se deve reconhecer a inocorrência de risco nulo. Se o risco é nulo, a atividade não existe.
Os eventos futuros e incertos podem trazer tanto riscos quanto oportunidades. A praxe, no entanto, é a tomada da noção de risco com o sentido que remete à advertência e ao cuidado, e não à oportunidade, mais afeta a outros processos de planejamento e análise de custo benefício (COMMITTEE OF SPONSORING ORGANIZATIONS OF THE TREADWAY COMISSION - COSO, 2004).
Assim, havendo a possibilidade de um evento ocorrer, há a chance de se desencadear consequências que se quer ver medidas e evitadas. Evento, portanto, é a ocorrência fenomênica que pode determinar consequências que impactam no atingimento de um objetivo.
A noção intuitiva de risco está presente em toda atividade, norma ou precaução tomada para prevenir um mal, para que se proteja um valor, um objetivo ou uma política. Não é desta noção intuitiva, no entanto, que se trata o “processo de gerenciamento de risco”.
4. O PROCESSO DE GERENCIAMENTO DE RISCOS
O processo de gerenciamento de riscos é uma atividade sistemática, conscientemente coordenada para o levantamento, avaliação, tratamento e estudo, de modo cíclico, para diminuir a incerteza na realização de objetivos. Sem isso não há “processo de gerenciamento de riscos”, muito embora possa haver, esporádica e intuitivamente, considerações subjacentes sobre riscos em decisões, normativos e políticas.
Como o gerenciamento de riscos corporativos envolve atividade consciente e organizada de análise de objetivos, análise da realidade contextual, levantamento de hipóteses, raciocínio e processamento de informações, é uma atividade que envolve considerável concentração e sinergia de grupo. Por este motivo, organizações que não possuem cultura de planejamento e forte accountability têm dificuldade em implementar um processo efetivo de gerenciamento de riscos.
O Sumário Executivo do Gerenciamento de Riscos Corporativos do Committee of Sponsoring Organizations of the Treadway Comission - COSO (2013) estabelece como componentes do gerenciamento de riscos corporativos, multidirecional e interativo:
1) o ambiente interno à organização, em que as atividades ocorrem e que determina a liderança e os valores;
2) a fixação de objetivos, que serão protegidos pela identificação de eventos e pelo tratamento dispensado aos riscos;
3) identificação de eventos;
4) avaliação de riscos, compreendendo a análise da probabilidade e impacto dos eventos nos objetivos, considerados em sua inerência e, após vistos os controles, em sua residualidade;
5) resposta ao Risco;
6) atividades de controle;
7) informações e comunicações e;
8) monitoramento.
Este artigo abrange somente a fase de análise dos riscos e, especificamente, a escala apropriada para a avaliação do impacto e da probabilidade de um evento ocorrer.
5. PROBABILIDADE E IMPACTO, OU CONSEQUÊNCIA
A probabilidade é a “chance de algo acontecer” (ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS, 2009). Esta probabilidade pode ser descrita de muitas formas, qualitativa ou quantitativamente. A utilidade de uma definição quantitativa da probabilidade exsurge da maior possibilidade da integração da grandeza com outras fases do gerenciamento de riscos e outras fases do próprio sistema de gerenciamento de riscos.[3]
O impacto é a severidade, ou as consequências danosas ao atingimento do objetivo. Assim como a probabilidade, o impacto de um evento pode ser descrito qualitativa ou quantitativamente, no sentido de se medir o quanto o evento atrapalhará a consecução do objetivo.
6. ESCALAS DE PROBABILIDADE E ESCLAS DE IMPACTO E O PROBLEMA DA DIFERENCIAÇÃO
Há várias formas de se fazer a quantificação das escalas de avaliação do impacto e da probabilidade da ocorrência de eventos. Utiliza-se uma simples sequência de números que variam geralmente entre 0 e 5, ou 6; números pares (2, 4, 6, 8, 20), ou números escolhidos arbitrariamente.
Há, algumas vezes, a necessidade de se inserir uma interface de ponderação, para que haja diferenciação suficiente entre as grandezas avaliadas. Foi o que fez, recentemente o Tribunal de Contas da União no Roteiro de Avaliação de Maturidade da Gestão de Riscos (BRASIL, 2018b), a ser utilizado para avaliar a maturidade da gestão de riscos das organizações públicas, bem como para identificar possibilidades de melhorias. O roteiro observa que a “relação simples pode não refletir relações não lineares, sendo necessário, assim incluir um fator de ponderação para uma das duas variáveis (probabilidade ou impacto, de modo a atingir a escala relativa necessária entre eles) e ou um operador exponencial para uma ou para ambas as variáveis.” Tal providência, contudo, torna ainda mais difícil e completa a avaliação e, cremos, a escala aqui mais adiante proposta torna esta providência menos necessária.
Quanto às escalas de probabilidades e impacto (consequências), o TCU utiliza os “pesos” 1, 2, 5, 8 e 10. A escala de probabilidades varia quanto à ocorrência improvável, rara, possível, provável ou praticamente certa. A escala de impacto varia de impacto mínimo, pequeno, moderado, significativo e catastrófico (BRASIL, 2018a). Esta escala já representa uma melhoria em relação a escalas mera- mente compostas de números sequenciais como 1, 2, 3, 4, 5 ou 2, 4, 6, 8, 10, mas, mesmo assim, pode ser difícil a diferenciação entre as grandezas 1 e 2 ou entre um 8 e 10, a depender dos critérios utilizados. É também complicada a escolha entre um impacto mínimo e pequeno, ou moderado e significado. A semelhança linguística das palavras empregadas é um fator que pode impactar na precisão das avaliações, mormente quando se trata de avaliações intuitivas.
Há, portanto, problemas de diferenciação entre as escalas, bem como ausência de aceleração coerente, ou seja, as escalas geralmente utilizadas apresentam ausência de aumento coerente da grandeza à medida que a série aumenta.
Outro fator que se observa nas escalas acima referidas é a produção de uma matriz sem coerência suficiente para o agrupamento de faixas de risco.
7. O RISCO INERENTE
Risco inerente é o risco “bruto”, tomado em sua forma isolada, sem considerá-lo num contexto de tratamentos e controles. Risco inerente é uma medida obtida pela multiplicação da escala do impacto pela escala da probabilidade, resultando num número ou sinal que expressa a magnitude de determinado risco “bruto”.
Uma vez obtido o risco inerente, pode-se incluí-lo em uma matriz com predefinições que já determinem de alguma forma inicial a intensidade de resposta aos riscos levando-se em conta, inclusive, o apetite ao risco, análises de custo-benefício e toda uma política da organização.
Cada organização pode estabelecer suas próprias escalas de probabilidade e impacto, bem como seus próprios limites e formas de resposta aos riscos baseadas em sua constituição real.
A escala para avaliação de probabilidade e impacto sugerida pelo TCU produz a seguinte Matriz (BRASIL, 2018a, p. 42):
Figura 1 - Matriz de Riscos utilizada pelo TCU

Fonte: Brasil (2018a)
A escala utilizada pelo TCU produz valores próximos entre al- gumas categorias, como os graus extremos (80/100), ou entre graus médios (50-64). O mesmo acontece com os graus baixos, que variam de 1 a 8 (BRASIL, 2018a).
A depender da profundidade e sofisticação das definições de apetite a risco, é importante que haja uma matriz que, ao mesmo tempo, possa prover uma comparabilidade prontamente captada pe- los sentidos humanos e uma coerência interna na formação de uma matriz derivada de um sistema de coordenadas cartesianas. Não só deve haver coerência de sentido no eixo das abscissas e eixo das ordenadas, mas também coerência na própria matriz, em suas dia- gonais e transversais. Tal coerência, conforme demonstraremos, é provida pela utilização da sequência de Fibonacci para a elaboração da matriz de riscos.
8. A ESCALA DE FIBONACCI
Existem centenas de sequências, com os mais diversos efeitos e aplicações. A busca de escalas e sequências matemáticas que sejam simples e que produzam diferenciação entre os números, coerência interna quando dispostos em matriz e que tenham um claro efeito didático não é trivial.
A sequência de Fibonacci[4] pode ser utilizada com sucesso para a avaliação de impacto e probabilidade de eventos, pelos motivos que serão expostos mais adiante.
Para uma compreensão inicial basta que se saiba que a sequência de Fibonacci é aquela em que um dado número é a soma dos dois anteriores e pode ser expressa da seguinte maneira: 0, 1, 1, 2, 3, 5, 8, 13, 21 ...
Segundo Koshi (2018, p. 8), a definição recursiva é a seguinte:
F1 = F2 = 1 – condição inicial (isso explica a repetição do número 1 da sequência de Fibonacci e marca o início da sequência).
Fn = Fn-1 + Fn-2 (recorrência), onde n maior ou igual a 3.
Podemos perceber que, na sequência de Fibonacci, os números possuem uma relação entre si, dada pela existência de números ante- riores. Disso resulta uma direta comunicação entre os números, em uma escala previsível em que as grandezas são relacionadas muito naturalmente, com pouquíssima regra externa que não a regra acima mencionada.
Esta sequência é utilizada por todo o mundo natural na or- ganização de incontáveis estruturas, desde o DNA. O girassol, por exemplo, tem a estrutura de suas sementes em espirais que refletem a sequência de Fibonacci. Diversas flores e plantas têm suas pétalas e folhas baseadas nessa sequência. A organização de colmeias de abelhas, e até o mundo atômico utiliza-se desta sequência. (KOSHI, 2018, p. 7-35).
Há, entre os números da sequência de Fibonacci, uma relação chamada de “razão áurea”, ou “proporção áurea”. A demonstração matemática desta proporção áurea escapa ao objetivo deste trabalho, mas pode-se dizer que dois números estão em razão áurea se sua ra- zão é igual à razão de sua soma pela maior das quantidades. Ou, em termos mais simples, a razão entre dois números de Fibonacci tende a produzir números como 1,625, ou 1,61818, ou 1,6180339… ou seja, muito simplificando, 1.6.
Esta razão está presente em várias relações da natureza, artes, galáxias, corpo humano, etc. (KOSHI, 2018, p. 301).
Esta proporção harmônica, mas diferençável, é que produzoda a coerência de uma matriz de riscos baseada na escala de Fibonacci.
9. AVALIAÇÃO QUANTITATIVA DE EVENTOS DE RISCO
É deveras difícil atribuir, arbitrariamente, números a uma situação, problema ou consequências com o fim de compará-los.
Este problema atributivo é enfrentado por diversos campos de conhecimento e práticas de administração. Uma interessante área em que se busca esta atribuição é o planejamento, em suas diversas ver- tentes. Previsões e comparações entre o tamanho de projetos e previsões de recursos dependem de uma atribuição preditiva de tamanho, pesos e importância.
Em todas essas atividades em que se procura atribuir uma grandeza numérica a um evento natural não prontamente quantificável há a necessidade de atribuição arbitrária de valores.
A criação de balizas lógicas para enquadramento ajuda, mas, mesmo assim, é muito difícil a diferenciação entre números em sequência, pois o raciocínio carece de balizas comparativas. Como se diferenciariam, por exemplo, um risco 3, ou um 4, numa escala de 1 a 10? É difícil dizer.
Os métodos de pesquisa de opinião há muito também enfrentam o desafio exposto acima, pois necessitam de atribuição quantitativa a problemas muitas vezes qualitativos.
A primeira e mais conhecida escala de avaliação de questionários é a escala Likert. Ao responder a um item, o respondente escolherá em uma escala de concordância ou discordância que vai de 1 a 5 (1. discorda fortemente, 2. discorda, 3. nem concorda nem discorda, 4. concorda. 5. concorda fortemente) (LIKERT, 1932). A crítica aponta que esta escala está propensa a distorções de muitas espécies, mas até hoje é um padrão de organização das pesquisas de opinião.
Uma das principais conclusões que se pode chegar é que a existência de 5 graus de avaliação é suficiente e desejável para se perscrutar uma opinião. Mais do que 5 graus pode ser exagero, e menos, pode ser uma simplificação indesejável.
Sendo assim, defende-se aqui a existência de 5 escalas de avaliação de probabilidade e 5 escalas para o impacto do evento de risco como suficientes para uma boa análise de riscos.
Com relação à utilização da sequência de Fibonacci, observa-se que a proximidade dos quatro primeiros números com a definição necessária para o início da sequência de Fibonacci (0, 1, 1, 2), e propõe-se que se comece pelo número 3, pois que a partir dele a sequência não se repete e é suficientemente distinguível. A sequência também produz aceleração e quantidade suficiente que facilita a comparação. Riscos que poderiam ser classificados como 0, 1 e 2 serão tidos como insignificantes. A escala seria composta então de 3, 5, 8, 13 e 21.
Figura 2 - Exemplo de Escala de probabilidade e impacto
utilizando-se a
sequência de Fibonacci
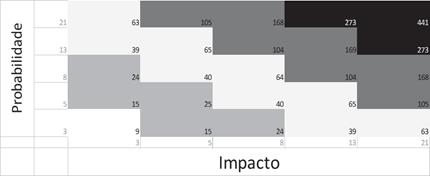
FONTE: Autoria própria
Nesta definição de graus de risco proposta para fins didáticos (pois pode e deve variar de acordo com a política de gestão de risco e apetite de risco das organizações), os limites são os seguintes:
• 9 - Risco baixíssimo.
• 15, 24, 25 - Risco Baixo (observa-se claramente duas faixas de risco baixo).
• 39, 40, 63, 64, 65 - Risco Médio (observa-se duas faixas de Risco Médio).
• 104, 105, 168, 169 - Risco Alto (observa-se duas faixas de Risco Alto).
• 273, 441 - Risco Extremo (duas faixas de Risco Extremo).
A depender da abordagem que a organização der ao processo de gerenciamento de riscos, a matriz pode ser dividida em faixas diferentes de classificação de riscos, podendo variar devido ao apetite a riscos e à forma de respostas aos riscos.
10. VANTAGENS DA UTILIZAÇÃO DA SEQUÊNCIA DE FIBONACCI PARA GERAÇÃO DE MATRIZ DE RISCOS
A utilização da sequência de Fibonacci se mostra extremamente útil para a avaliação de probabilidade e impacto de um evento. Considere as razões abaixo para a demonstração das vantagens sob vários pontos de vista:
11. PERCEPÇÃO MAIS NATURAL DAS DIFERENÇAS NA ESCALA E COERÊNCIA INTERNA DAS FAIXAS DE RISCO
Entendemos por faixa de risco os produtos da multiplicação dos índices de probabilidade e impacto que se enquadrem em uma classificação (risco irrelevante, risco baixo, risco médio, risco alto, etc).
Nas faixas exemplificativas acima propostas, as diferenças percentuais entre os valores de variação dos riscos baixíssimo, baixo, médio, alto e altíssimo são de 66,67%, 66,67%, 62,5%, 61,54%, uma diferença razoável dentro de uma mesma classe de risco que se aproxima da proporção áurea já citada (girando em torno de 1.6). Tal descoberta é relevante, significando que os valores mantidos nesta faixa não agridem a coerência numérica que já faz parte da lógica e cultura humana, agregando elegância e coerência à escala.
Para exemplificar, toma-se a escala adotada 1, 2, 5, 8, 10 com a nossa definição de faixas de risco e obtêm-se entre as mesmas classes (divididas de acordo com as mesmas definições aqui adotadas) as seguintes diferenças: 150% (2-5), 212,50% (8-25), 220% (20-64) e 25% (80-100):
Pode-se também fazer uma análise nas faixas diagonais, agregando-se da seguinte forma:
Figura 3 - Faixas diagonais de uma Matriz de Risco a partir da
sequência 1, 2, 5, 8, 10
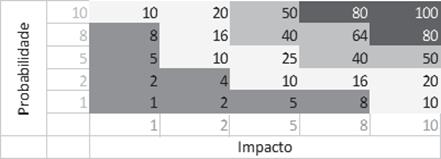
Fonte: Autoria própria
Esta sequência produz diferenças dentro de uma mesma “faixa” da seguinte magnitude: 700% (1-8), 150% (10-25), 60% (40-64) e 25% (80-100). Essa diferenciação, ao ir diminuindo à medida que o risco aumenta, vai de encontro ao que a intuição da avaliação de risco sugere, pois os impactos de uma faixa considerada muito baixa não deveria variar tanto (700%), nem uma faixa de risco muito alta variar tão pouco (25%) já que geralmente riscos mais críticos costumam ter resultados muito mais agudos do que riscos em faixas mais amenas.
Assim, em termos de coerência interna dos índices, a utilização da Sequência de Fibonacci para a construção da Matriz de Riscos traduz vantagens importantes em termos de diferenciação de faixas e coerência entre uma mesma faixa, propiciando uma análise muito mais coerente dentro de uma mesma faixa. Tal harmonia numérica facilita o enquadramento dos eventos em determinada faixa de risco afim, e uma melhor escolha do tratamento proporcional a cada faixa de risco (resposta ao risco).
12. MELHOR COMPARABILIDADE E DIFERENCIAÇÃO ENTRE AS GRANDEZAS
A sequência de Fibonacci proporciona uma melhor comparabilidade entre as grandezas. É muito mais fácil perceber a diferença entre 2 e 5, ou entre 5 e 8 do que entre 2 e 4, ou 8 e 10. Sutherland (2014, p. 93), ao analisar estimativa de grandezas para planejamento de trabalho em equipe sustenta que: “nós humanos somos absolutamente terríveis” em projeções, mas somos relativamente bons em tamanhos relativos. O ideal seria utilizarmos tamanhos relativos de objetos que já conhecemos, mas há vantagem de utilizar a sequência de Fibonacci, pois é um padrão ubíquo em sistemas naturais, sendo que os humanos têm milênios de experiência nisso.
Os números na sequência de Fibonacci estão tão distanciados que nós podemos facilmente dizer a diferença. É fácil para as pessoas decidir-se por um lado ou outro. Se uma pessoa estima algo em cinco, e outra em oito, nós podemos intuitivamente ver a diferença. Mas e a diferença entre cinco e seis? É muito sutil, mais do que nosso cérebro pode realmente registrar. (SUTHER- LAND, 2014, p. 94).
Observe-se os números não repetidos retirados de uma matriz de risco de 5 níveis utilizando-se a escala de Fibonacci a partir do 3:
Figura 4 - Números não repetidos em uma Matriz de Risco,
elaborada a partir da Escala de Fibonacci
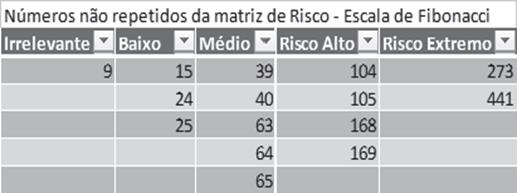
Fonte: Autoria própria
Observe-se, agora, o gráfico gerado para comparação:
Figura 5 - Comparabilidade dos números da Matriz elaborada
a partir da Escala de Fibonacci
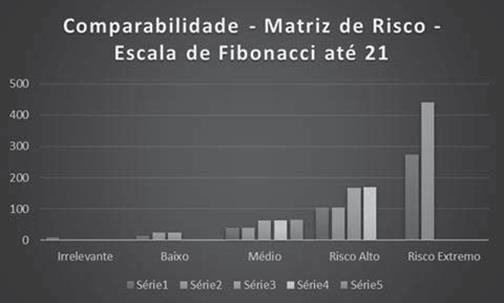
Fonte: Autoria própria
Compare-se o gráfico acima com um gráfico gerado utilizando a escala 1, 2, 5, 8, 10:
Figura 6 - Números não repetidos de Matriz elaborada a partir
da Escala de Fibonacci
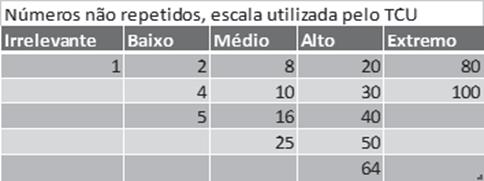
Fonte: Autoria própria
Figura 7 - Comparabilidade da Escala 1, 2, 5, 8, 10
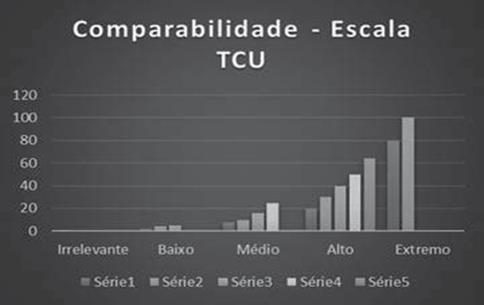
Fonte: Autoria própria
13. CRESCIMENTO NÃO LINEAR DA SEQUÊNCIA
Outra vantagem da sequência de Fibonacci na construção da matriz de riscos é que há um crescimento exponencial constante da escala. As grandezas aumentam relativamente com o aumento dos valores. Eis dois gráficos utilizando-se a sequência de Fibonacci e outra uma sequência linear.
Figura 8 - Crescimento da Matriz de Risco utilizando a escala
de Fibonacci
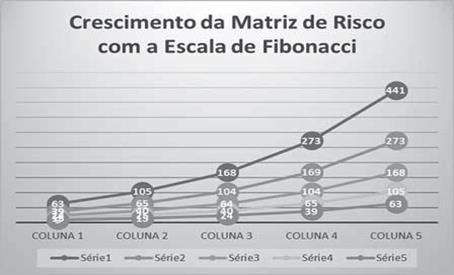
FONTE: Autoria própria
Figura 9 - Crescimento da Matriz de Risco com uma escala
Linear
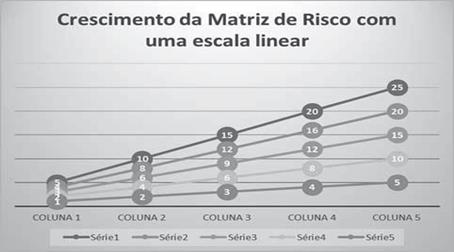
FONTE: Autoria própria
O efeito que se observa é uma espécie de “aceleração” em que os valores maiores são significativamente mais relevantes que os menores, o que torna a escala apropriada para a avaliação de riscos.
14. PREVISIBILIDADE DOS NÚMEROS SEGUINTES NA ESCALA
Outro efeito é que a sequência de Fibonacci é previsível quanto aos próximos números da sequência e provê a certeza da manutenção das propriedades da matriz. Tal previsibilidade é útil para que a inovação na adoção de novas grandezas não signifique uma ruptura com o sistema anterior adotado e servirá também para a manutenção da coerência em sistemas computacionais.
15. UTILIZAÇÃO DE AUXÍLIO VISUAIS NO PROCESSO DE AVALIAÇÃO DE RISCOS
Para finalidades práticas nos exercícios corporativos de avaliação de riscos, a razoabilidade e factibilidade das comparações são aumentadas grandemente com o auxílio de gráficos. O processo mental de avaliação deriva grande vantagem da possibilidade de comparação visual entre grandezas. O processo de avaliação de riscos, obviamente, se beneficia grandemente se forem empregados auxílios visuais para a imputação de grandezas à probabilidade, ao impacto e à própria matriz de riscos.
16. AUXÍLIOS VISUAIS PARA A PROBABILIDADE
A importância da sequência de Fibonacci para a estimativa de probabilidade é aumentada quando se utiliza algum auxílio visual para os exercícios de avaliação de riscos. Sugere-se a utilização da própria quantidade (números) da escala para indicar a probabilidade. A criação de gráficos com 3, 5, 8, 13 ou 21 objetos pode passar muito bem a ideia de quantidade, conforme se demonstra na figura abaixo:
Figura 10 - Auxílio visual para estimativa da probabilidade
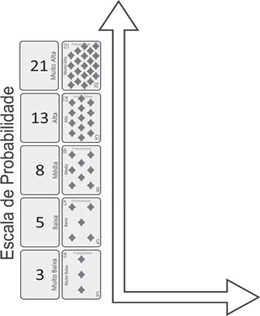
FONTE: Autoria própria
Para exercícios conjuntos, ou mesmo individuais, de identifi- cação de riscos, tal auxílio se mostra muito útil para aguçar a per- cepção da probabilidade de ocorrência de um evento. Para exercícios utilizando-se alguma adaptação da técnica Delphi, por exemplo, es- tes auxílios visuais auxiliam a planificar as noções de probabilidade. Ao obedecer às proporções quantitativas da sequência de Fibonacci, este auxílio visual se aproveita dos efeitos biológicos que tal escala provoca, facilitando o acerto da estimação.
17. AUXÍLIOS VISUAIS PARA O IMPACTO
A noção de impacto também pode ser ilustrada
utilizando-se gráficos apropriados. Sugere-se a utilização de gráficos,
passando noção de dano ou efeito. É importante que tal auxílio incorpore a
escala gráfica da sequência de Fibonacci, e que cada sinal gráfico seja
comparado com outros que expressam outras severidades. Tal método é
especialmente apropriado para os exercícios de atribuição de valores a impacto
a partir de fatores qualitativos.
Figura 11 - Auxílios visuais para a avaliação dos impactos dos eventos
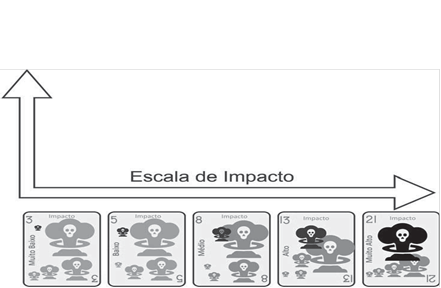
FONTE: Autoria própria
18. AUXÍLIOS VISUAIS PARA A MATRIZ DE RISCOS
É importante também que a própria matriz de riscos tenha uma representação didática apropriada, devendo servir para auxiliar o avaliador a enquadrar apropriadamente o evento de risco em uma determinada faixa de risco. Eis abaixo um exemplo de uma matriz de risco com este objetivo, incorporando já os auxílios da escala de probabilidade e de impacto, gerando uma matriz que remete à atenção e à advertência:
Figura 12 - Matriz de riscos de riscos com arredondamentos
e auxílios visuais
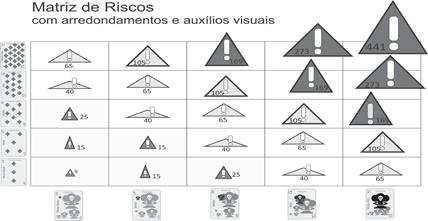
FONTE: Autoria própria
Outra forma de se apresentar a matriz de risco, dando apenas uma noção relativa das grandezas baseadas na sequência de Fibonacci.
Figura 13 - Matriz de Riscos com demonstração das grandezas da escala de Fibonacci
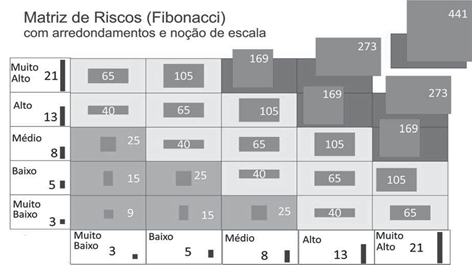
FONTE: Autoria própria
19. PROPOSIÇÃO DE PROCEDIMENTO SIMPLIFICADO PARA OBTENÇÃO DO RISCO RESIDUAL
Segundo a "Government Accountability Office" (GAO) dos Estados Unidos, o risco inerente é o risco a que está sujeita uma entidade na ausência de resposta da administração ao risco. Como já dissemos, é o risco “bruto”. Risco residual é o risco que permanece depois da gestão implementar respostas ao risco inerente. Pode-se afirmar que é o risco “líquido”. Risco residual, portanto, é o risco que, a depender do apetite a risco e da estratégia, ainda precisa ser tratado (UNITED STATES OF AMERICA, 2014).
O Tribunal de Contas da União (BRASIL, 2018a, p. 29-31) utiliza para a obtenção do risco residual a partir de um determinado risco inerente, uma operação contendo 5 fases.
1) a partir da valoração da probabilidade e impacto, chega-se a um risco inerente, desprezando-se controles;
2) considera-se os controles existente avaliando-se o nível de confiança de que o controle mitiga deter- minado risco, atribuindo-se um número para um nível de confiança forte (0,8) até uma confiança inexistente (0,0);
3) obtém-se um “risco de controle”, inversamente proporcional à avaliação do nível de confiança no sentido de que se o nível de confiança é 0,0, o risco de que o controle não mitigue esse risco é pleno (1,0), graduando-se até que o risco de que o controle não mitigue o risco seja baixo (0,2);
4) aplicando-se este valor ao risco inerente se chega a um número que, por último, é comparado nova- mente a uma matriz, gerando um risco residual.
Apesar de tal metodologia cumprir com o objetivo de propiciar a obtenção de um risco residual após o exercício mental de considerar controles, mitigando um risco inerente, possui a desvantagem de perder contato, já na segunda fase, justamente com os fatores utiliza- dos para a formulação do risco, ou seja, a probabilidade e o impacto. Propõe-se que esta operação seja substituída pelo exercício de avaliação direta de como determinado controle diminui a probabilidade, ou o impacto, ou ambos de uma só vez.
Considerando-se cada probabilidade e impacto de um risco inerente, deve-se analisar se determinado controle ou atividade diminui a probabilidade e/ou o impacto em que medida chegando-se imediatamente a um risco residual mais bem definido. Há ainda es- paço para que se considere a qualidade do controle atuando sobre determinado risco, mas não indiretamente sobre a matriz produzida, mas diretamente sobre a probabilidade e impactos do risco inerente.
Se uma probabilidade for considerada 21, utilizando-se a sequência de Fibonacci de 5 sequências, um controle inexistente não diminuiria em nada esta probabilidade. Também não diminuiria a probabilidade de um controle, cuja própria natureza não atuasse sobre este fator. Se houver, por outro lado, um controle considerado “bom” sobre a probabilidade, pode-se considerar esta diminuída de 21 para 8, por exemplo.
O mesmo acontece com o impacto. Na formação do risco inerente, determinado impacto é considerado de magnitude 21. Se o controle em nada diminui o impacto, por sua natureza ou por ineficiência, em nada modifica o impacto residual. Se, contudo, o controle for “bom”, pode-se considerar que diminui medianamente um impacto para uma grandeza 8, por exemplo.
A depender do apetite a risco da organização, avalia-se se o risco residual precisa ou não de tratamento.
Este método tem a virtude de permitir uma maior compreensão da natureza do controle e sua influência sobre os riscos. Também permite uma maior largueza de definições sobre o que é, para deter- minada atividade ou processo, um controle excelente, ótimo, bom, fraco ou mesmo inexistente. Abre-se, portanto, toda uma possibilidade de qualificação dos controles sem que precise haver uma padronização que, devido à grande diversidade de medidas possíveis, é indesejável.
Simplifica-se, assim, o processo de avaliação dos controles ao mesmo tempo em que se aumenta o conhecimento sobre o próprio controle existente ou necessário à mitigação do risco.
Eis abaixo uma tabela sugestiva da análise da efetividade de um controle sobre um risco inerente partindo-se da avaliação direta na probabilidade e no impacto, que chamamos de probabilidade residual e impacto residual, baseados na sequência de Fibonacci.
Figura 14 - Probabilidade residual – efetividade dos controles sobre a probabilidade do risco inerente
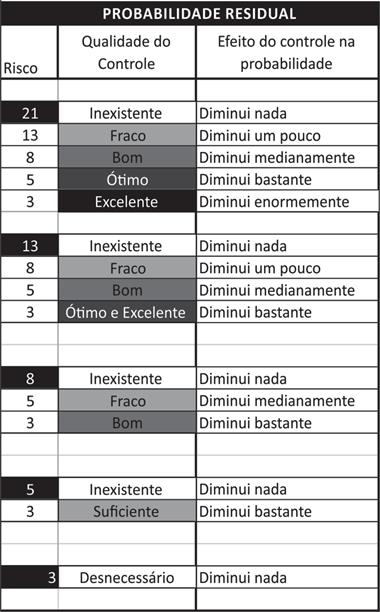
FONTE: Autoria própria
Figura 15 - Impacto residual – efetividade dos controles sobre a probabilidade do risco inerente
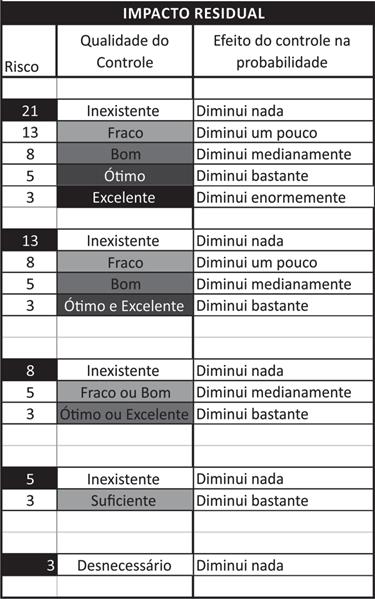
FONTE: Autoria própria
Esta forma clara e didática de obtenção do risco residual através da crítica direta dos controles sobre a probabilidade e impacto que formam o risco inerente, somada à utilização da sequência de Fibonacci e com os auxílios visuais, geram uma metodologia de avaliação de risco didática e competente para os fins aos quais se destina esta etapa do gerenciamento de riscos.
20. CONCLUSÕES
Conclui-se, assim, que a utilização da sequência de Fibonacci para a avaliação do impacto e da probabilidade da ocorrência de um evento é uma boa alternativa a outras escalas meramente sequenciais ou arbitrárias. A sequência de Fibonacci provê coerência interna entre as faixas de risco (dentro dos limites aproximados da proporção áurea) e favorece a comparabilidade, tanto nos eixos das escalas de probabilidade e impacto, quanto dentro do agrupamento das faixas de risco escolhidas. Esta escala propicia também previsibilidade dos próximos valores da escala de impacto e probabilidade, facilitando coerência dos sistemas e evitando a obsolescência dos trabalhos anteriores.
A utilização de gráficos coerentes com a sequência de Fibonacci é de grande auxílio para o processo mental de enquadramento e atribuição de valor numérico a determinado evento, e pode auxiliar exercícios conjuntos de avaliação de riscos, produzindo resultados mais coerentes e proporcionais.
Por fim, considerar diretamente como os controles e medidas atuam na probabilidade e impacto que formam o risco inerente para chegar-se, a partir da eficácia do controle, a uma probabilidade e impacto residuais, gerando-se então um risco residual mais delimitado e definido é uma boa prática que simplifica o processo de avaliação de riscos e gera mais conhecimento sobre a própria atuação dos controles.
A contribuição trazida por este artigo pode auxiliar as organizações, principalmente as organizações públicas, a conferir maior agilidade, segurança, coerência e rapidez no processo de gestão de riscos, representando economia de recursos e melhoria na governança institucional.
4. REFERÊNCIAS
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS - ABNT.
NBR - ISO 31000. Gestão de riscos: princípios e diretrizes. Rio de Janeiro, 2009.
ALTOUNIAN, Cláudio Sarian; SOUZA, Daniel Luiz de; LAPA, Leonard Renne Guimarães. Gestão e governança pública para resultados: uma visão prática. Belo Horizonte: Fórum, 2017.
BRASIL. Tribunal de Contas da União. Secretaria Geral de Controle Externo. Referencial básico de gestão de riscos. Brasília, 2018a.
. Roteiro de auditoria de gestão de riscos, Brasília, 2018b.
. Roteiro de avaliação de maturidade da gestão de riscos. Brasília, 2018c.
COMMITTEE OF SPONSORING ORGANIZATIONS OF THE TREADWAY COMISSION – COSO. Enterprise Risk Management: Integrated framework : executive summary, 2004. Disponível em: <https://www.coso.org/Documents/COSO-ERM- Executive-Summary.pdf>. Acesso em: 22 ago. 2018.
. Internal control: integrated framework : executive Summary. 2013. Disponível em: <https://www.coso.org/ Documents/990025P-Executive-Summary-final-may20.pdf>. Acesso em: 22 ago. 2018.
INTERNATIONAL ORGANIZATION OF SUPREME AUDIT INSTITUTIONS - INTOSAI. INTOSAI GOV 9130 = Diretrizes
para Normas de Controle Interno do Setor Público : Informações adicionais sobre gestão de risco nas entidades. Vienna, 2004. [Endorsed on 2007].
KOSHI, Tomas. Fibonacci and Lucas Numbers with applications. 2nd. ed. New York: Wiley, 2018. v. 1.
LEICH, Matthew. Intelligent internal control and risk management: designing high-performance risk control systems. London: Gower, 2008.
LIKERT, Rensis. A technique for the measurement of attitudes.
Archives of Psychology, n. 140, p. 5-55, 1932. Disponível em:
<https://legacy.voteview.com/pdf/Likert_1932.pdf>. Acesso em: 22 ago. 2018.
SUTHERLAND, Jeff. SCRUM: the art of doing twice the work in half the time. New York: Crown Business, 2014.
UNITED STATES OF AMERICA. Government Accountability Office - GAO. Standards for internal control in the federal government. 2014. Disponível em: <https://www.gao.gov/ assets/670/665712.pdf>. Acesso em 22 ago. 2018.
2 [1] A teoria da agência busca analisar as relações em que a propriedade e o controle são designados a pessoas distintas, o que pode resultar em conflitos e custos resultantes dessa separação. A lógica da relação é a de que o “agente” (tomador de decisão) opte sempre pelas melhores alternativas do ponto de vista do “principal”, ou seja, buscando a maior agregação de valor, o que nem sempre acontece (ALTOUNIAN et al., 2017, p. 250).
3 [2] O dicionário eletrônico Houaiss define risco como: “probabilidade de insucesso de determinado empreendimento, em função de acontecimento eventual, incerto, cuja ocorrência não depende exclusivamente da vontade dos interessados”.
[3] A literatura coloca que o termo em inglês likelihood não possui equivalente em algumas línguas, por isso o termo “probabilidade” é utilizado.
[4] Fibonacci foi um matemático da idade média, nascido em 1170 em Pisa, Itália, estudioso no campo da aritmética e um dos influenciadores para a adoção do sistema de numeração indiana. A partir de problemas simples, Fibonacci descobriu sequências de números naturais que são de utilidade crescente para o entendimento de diversos fenômenos. Segundo Koshi (2018, p. 5), a sequência de Fibonacci veio de um simples experimento, conhecido como os Coelhos de Fibonacci. É formulado da seguinte forma: Suponha que haja dois coelhinhos recém-nascidos, um macho e uma fêmea. Encontre o número de coelhos produzidos em um ano se: 1) cada par leva um mês para se tornar maduro;
2) cada par produz um par misto a cada mês, começando com o segundo mês e; 3) os coelhos são imortais. Suponha-se por conveniência que o par original nasceu em 1 de janeiro, e, por levarem um mês para se tornarem maduros, ainda há apenas um par em 1º de fevereiro. Em março já se produz um par misto, em abril 3 pares, em maio 5 pares e assim por diante. (tradução nossa).